
はじめに
こんにちは、18卒のおでんとよばれているものです。 7月から看護のお仕事の実装をやっていく中、ABテストの検証結果待ち状態で新しい実装が着手できないという問題が発生しました。 これに対して、BayesianABテスト方法を提案してみところ、検証が終わるまでに2週間〜3週間かかっていたものが、わずか1週間で終えることができるようになりました。 今回は、その使い方について紹介したいと思います。
ABテストとは
Webサイトで画像や文章などをAパターンとBパターンの2パターンを用意して、どちらの方がよりユーザーに行動を促したを検証するものです。
Webマーケティングの施策検証方法の1つとして実施されています。
インターネット広告では、CV数(コンバージョン数)やCVR(コンバージョンレート)を高くすることが求められており、ABテストを実施して広告を出し分けるようにしています。
活用方法
A社のおでんの広告を使った時とB社のおでんの広告を使った時に、どちらのCV率(コンバージョン率)が高くなるかの施策をして、次のような結果が得られたとします。
ABテスト例
| クリック数 | CV数 | CVR | |
|---|---|---|---|
| ページA | 30000 | 425 | 1.42% |
| ページB | 28000 | 340 | 1.21% |
ABテストを実施して計測したCV数やCVRが、A社とB社の違いで本当に効果があるかどうかを検証する必要があります。
この検証をする際に、カイ二乗検定がよく使われています。
しかしカイ二乗検定には欠点がありサンプルサイズが小さい場合、効果があるかの判定が出にくいです。
ABテストサンプルサイズが小さい例
| クリック数 | CV数 | CVR | |
|---|---|---|---|
| ページA | 2255 | 32 | 1.42% |
| ページB | 1985 | 24 | 1.21% |
冒頭での、ABテストの結果待ち状態になっている課題の原因が、サンプルがたまるまでの時間が長いことでした。 このサンプルサイズの問題を解決したのが、BayesianABテストです!
ABテスト実戦
では実際に上の2つのデータを使って、カイ2乗検定とBayesianABテストを用いた検証を用いた検証をして比較してみたいと思います。 使う言語は、解析でよく使われているRを使います。
カイ2乗検定を用いた検証
カイ2乗検定とは
カイ2乗検定について例を元に説明したいと思います。 Webページでテストをした結果、以下の結果が得られたとします。
| ボタン押した | ボタンを押さなかった | |
|---|---|---|
| 赤いボタン | 70 | 180 |
| 青いボタン | 30 | 120 |
この時に、赤いボタンと青いボタンと関係があるかないかを検証できるのがカイ2乗検定です。 詳しい説明に関しては以下の参考サイトをみてください。
独立性の検定―最もポピュラーなカイ二乗検定 | ブログ | 統計WEB
サンプルサイズが大きい場合の検証
まずは、サンプルサイズが大きい例を使い検証をしてみます。
実行プログラム
> AB <- matrix(c(30000-425, 425, 28000-340, 340), ncol=2, byrow=T) #データを入力 > chisq.test(AB) #検証結果出力
検証結果
Pearson's Chi-squared test with Yates' continuity correction data: AB X-squared = 4.4033, df = 1, p-value = 0.03587
この結果で重要なのはこいつです → p-value p-valueは、有意確率と呼ばれています。カイ2乗検定では、有意確率が 0.05以下の場合、要因の違いによってCV数に効果を与えていると判断されています。
今回の結果では、p-value が 0.0359(有意確率が 0.05以下) でした。 この結果から、A社の広告を使った方がCV数が良くなると判定をすることができます。
サンプルサイズが小さい場合の検証
次にサンプルサイズが小さい例を使い検証をしてみます。
実行プログラム
> AB <- matrix(c(2255-32, 32, 1985-24, 24), ncol=2, byrow=T) #データを入力 > chisq.test(AB) #検証結果出力
検証結果
Pearson's Chi-squared test with Yates' continuity correction data: AB X-squared = 0.21426, df = 1, p-value = 0.6434
今回の結果では、p-value が 0.6434 でした。 この結果からは、別の広告を使ってもCV数に効果がないと判定されます。 このようにカイ2乗検定では、同じCVRであってもサンプルサイズが小さい場合、効果があるかの判定が出にくいと言われています。
BayesianABテストを用いた検証
BayesianABテストとは
BayesianABテストは、ベイズ推定の手法を取り入れた検証方法です。 事前確率と実際に得られたデータを元に、A社のおでんの広告がB社のおでんの広告に比べて何%の確率で良いかを検証をすることができます。 ベイズ推定については、参考書籍がとても分かりやすいのでぜひ合わせて読んでみてください。
参考書籍 完全独習 ベイズ統計学入門 著者 小島 寛之 2015/11/20
事前準備
BayesianABテスト用のパッケージを以下のコマンドでパッケージをインストールをします。
> install.packages("bayesAB")
ミラーサイトをどこにするかというメッセージが表示されたら、japanを選択をしてください。 インストールが完了したら準備は終わりです。
サンプルサイズが大きい場合の検証
先ほどと同じように、サンプルサイズが大きい例を使い検証をしてみます。
実行プログラム
> library(bayesAB) #パッケージ読み込み
> set.seed(10) #乱数固定
> A<-rbinom(30000,1,425/30000) #Aページのクリック数、CV数を入力
> B<-rbinom(28000,1,340/28000) #Bページのクリック数、CV数を入力
#ベルヌーイ分布の事前分布をベータ分布として初期パラメータを一様分布を仮定してa=1,b=1とし、シミュレーションを行う
> AB <- bayesTest(A,B,priors = c('alpha' = 1, 'beta' = 1),distribution = 'bernoulli')
> summary(AB) #検証結果出力
> plot(AB) # グラフ出力
検証結果
Quantiles of posteriors for A and B:
$Probability
$Probability$A
0% 25% 50% 75% 100%
0.01175708 0.01402836 0.01448583 0.01495520 0.01764696
$Probability$B
0% 25% 50% 75% 100%
0.009160405 0.011274530 0.011707422 0.012143179 0.014543185
--------------------------------------------
P(A > B) by (0)%:
$Probability
[1] 0.99852
--------------------------------------------
Credible Interval on (A - B) / B for interval length(s) (0.9) :
$Probability
5% 95%
0.09790378 0.39482144
--------------------------------------------
Posterior Expected Loss for choosing B over A:
$Probability
[1] 3.125861e-05
グラフ結果1
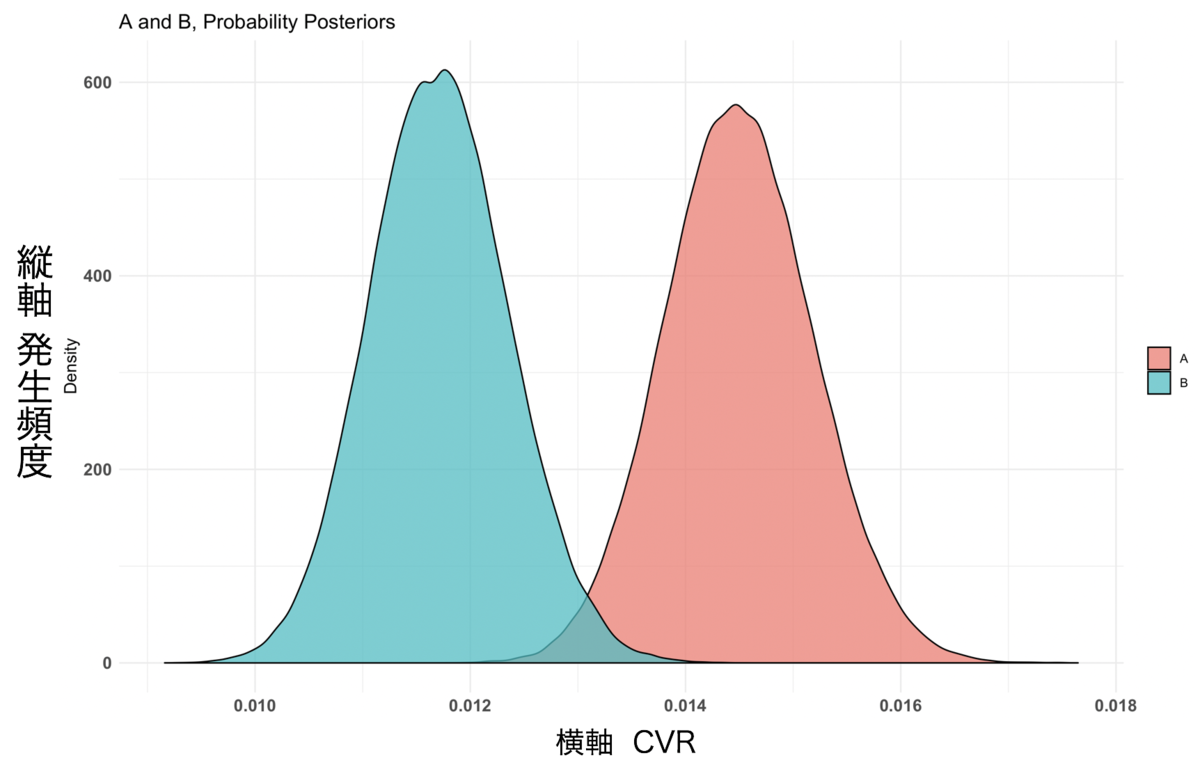
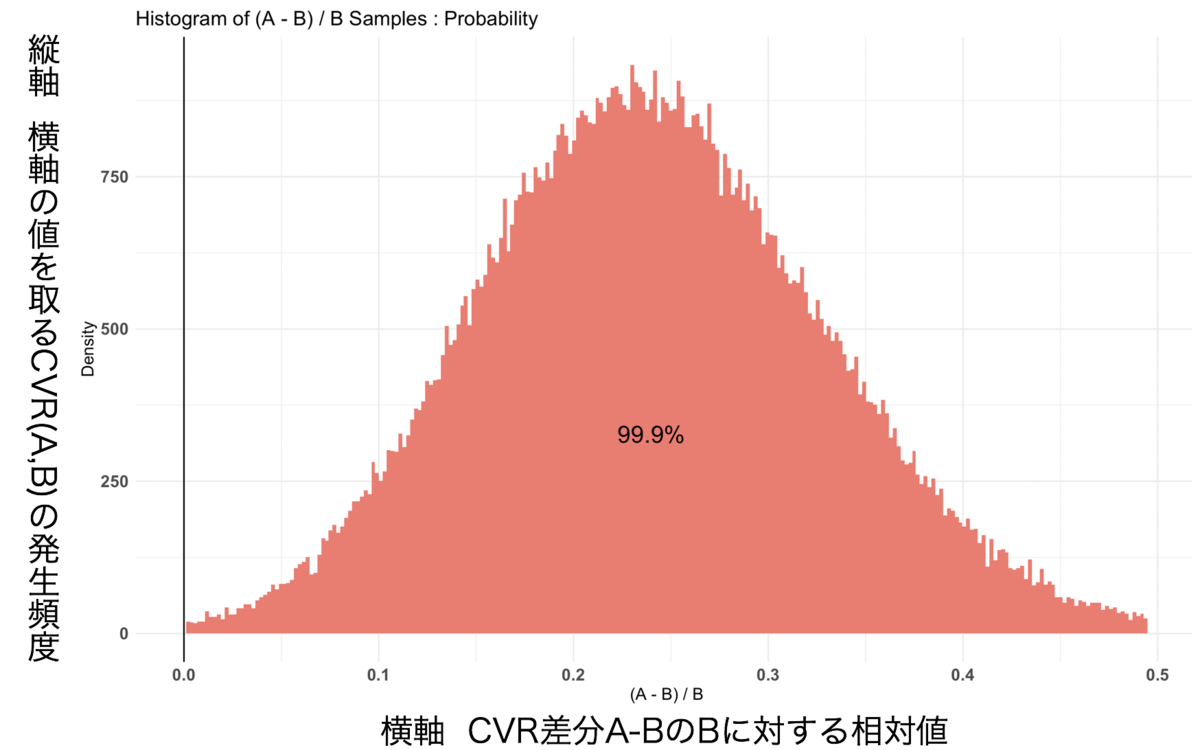
グラフ結果2
結果1
先ほど出力した結果の中で、最初に確認して欲しいのがP(A > B) by (0)%:の部分です。
この数字は、AのページがBのページよりもいい結果が得られる確率を表しています。
P(A > B) by (0)%: $Probability [1] 0.99852
今回の結果では、$Probability が 0.99852 でした。 グラフ結果1のCVRと発生頻度を注目すると、AとBの間に差が開いていることがわかります。 また、グラフ結果2はCVRの相対効果値を示したヒストグラムです。このグラフからは、ページAがページBよりもいい結果が得られる確率がどれぐらいあるかを確認をすることができます。
これらのことから、AページのCVRが99.9%の確率でBページよりもいい結果が得られるという判定ができます。
結果2
次に確認して欲しいのが Credible Interval on (A - B) / B ~ の部分です。
この数字は、信用区間(credible Interval)に対してどれぐらいの効果が見込まれるかを表しています。
Credible Interval on (A - B) / B for interval length(s) (0.9) :
$Probability
5% 95%
0.09790378 0.39482144
この数字がちょっとイメージがしにくいので図を作ってみました。
解釈図
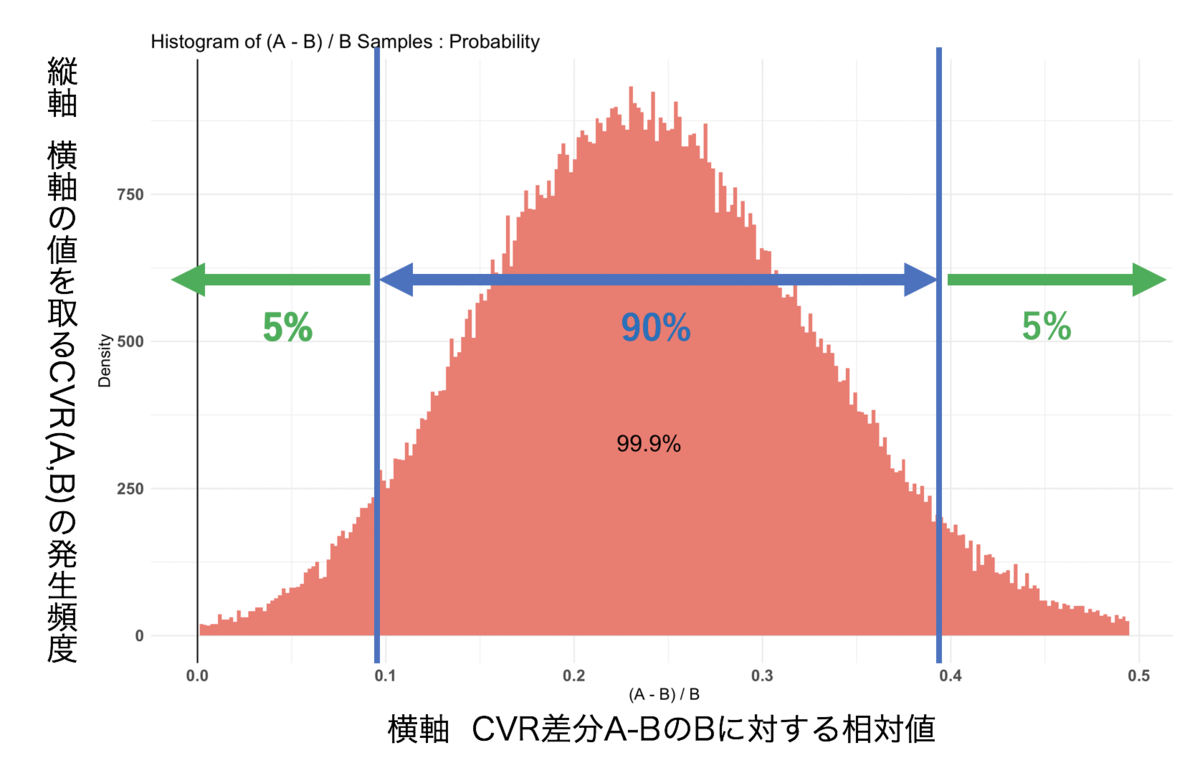
ここの数字では、CVRの効果が出る確率を示しています。
まず、5% 0.0979... は、AページをBページと比較した際に、Aページが109.7%以下の効果を出す確率が5%であることを示しています。
また、95% 0.394... は、AページをBページと比較した際に、Aページが139.5%以上の効果を出す確率が5%であることを示しています。
以上の結果から、AページをBページと比較した際に、Aページが90%の確率で109.7%〜139.5%の効果を出すと判定をすることができます。
サンプルサイズが小さい場合の検証
次にサンプルサイズが小さい例を使い検証をしてみます。
実行プログラム
> library(bayesAB) #パッケージ読み込み
> set.seed(10) #乱数固定
> A<-rbinom(2255,1,32/2255) #Aページのクリック数、CV数を入力
> B<-rbinom(1985,1,24/1985) #Bページのクリック数、CV数を入力
> AB <- bayesTest(A,B,priors = c('alpha' = 1, 'beta' = 1),distribution = 'bernoulli') #計算
> summary(AB) #検証結果出力
> plot(AB) # グラフ出力
検証結果
Quantiles of posteriors for A and B:
$Probability
$Probability$A
0% 25% 50% 75% 100%
0.007731823 0.015774076 0.017579264 0.019503243 0.032946183
$Probability$B
0% 25% 50% 75% 100%
0.004870983 0.011291718 0.012934394 0.014705932 0.027729893
--------------------------------------------
P(A > B) by (0)%:
$Probability
[1] 0.8921
--------------------------------------------
Credible Interval on (A - B) / B for interval length(s) (0.9) :
$Probability
5% 95%
-0.09560675 1.06632725
--------------------------------------------
Posterior Expected Loss for choosing B over A:
$Probability
[1] 0.01438976
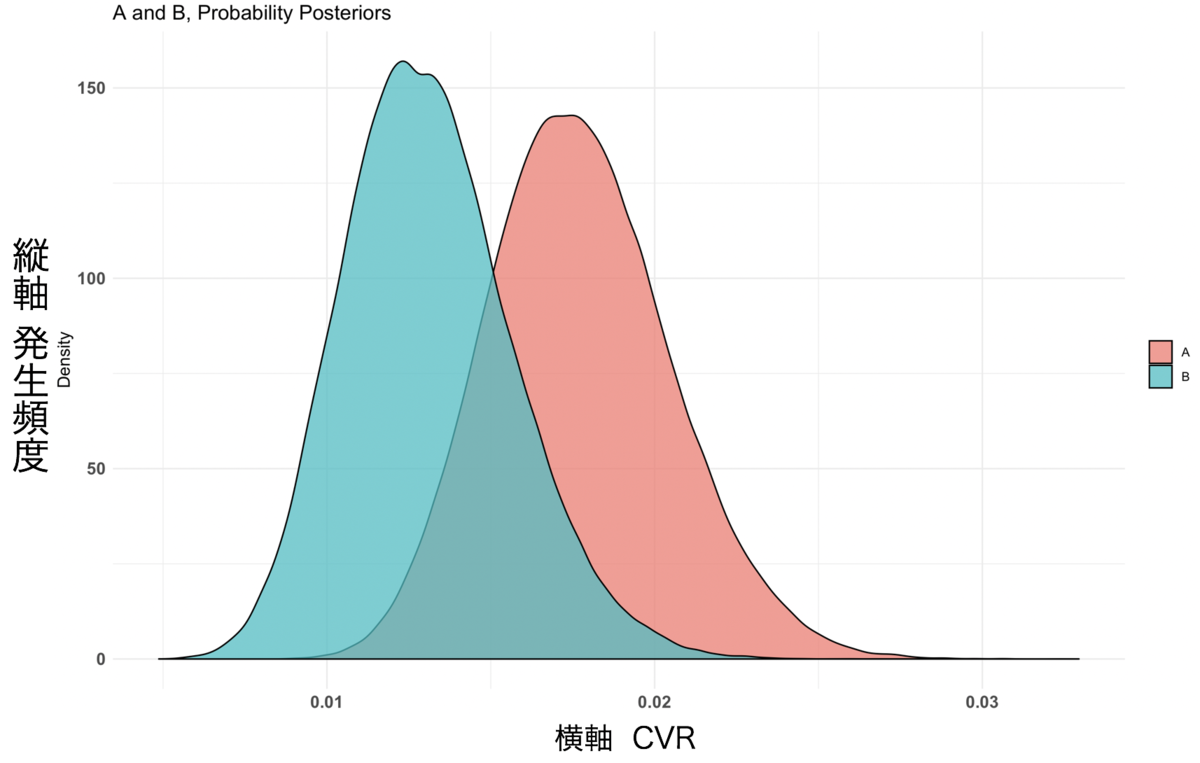
グラフ結果3
グラフ結果4
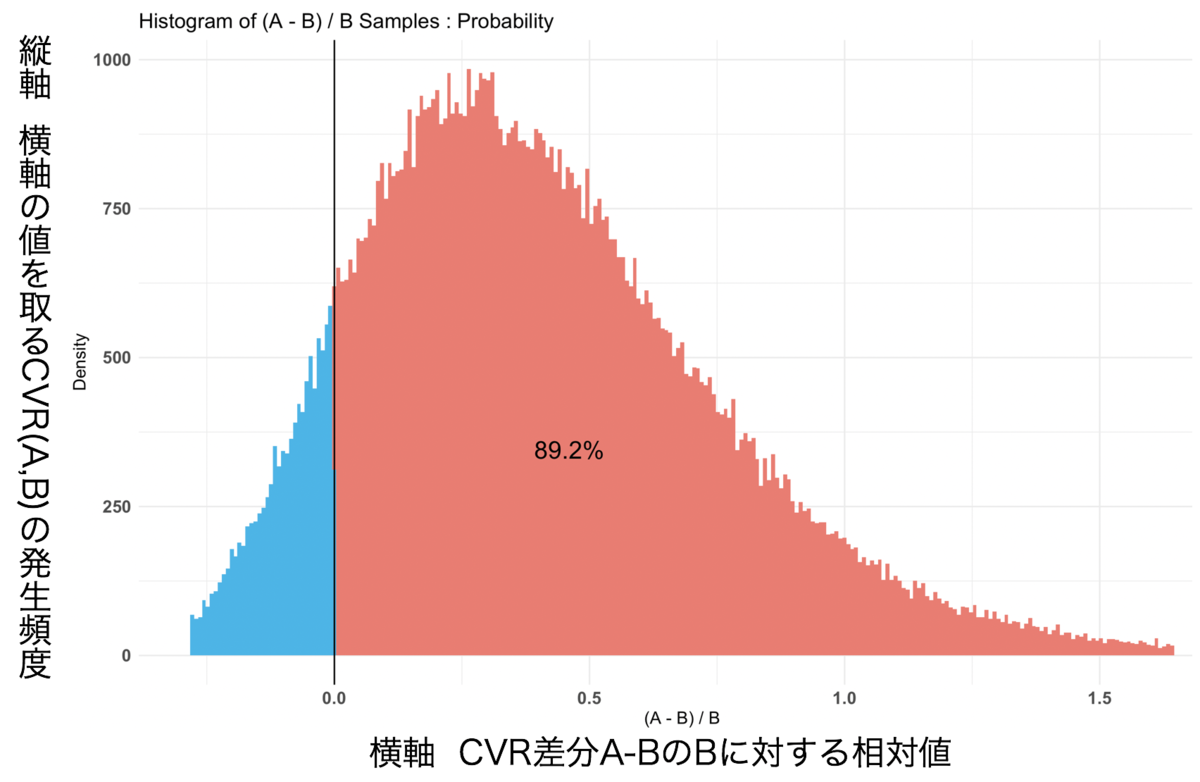
結果1
P(A > B) by (0)%: $Probability [1] 0.8921
今回の結果では、$Probability が 0.8921 でした。 グラフ結果3のCVRと発生頻度を注目すると、サンプルサイズが大きい時と比べて、AとBの間に差が開いていないことがわかります。 また、グラフ結果4のCVRの相対効果値に注目すると、ページAがページBよりもいい結果が得られる確率が89.2%であることが判断できます。
これらのことから、AページのCVRが89.2%の確率でBページよりもいい結果が得られるという判定ができます。
結果2
Credible Interval on (A - B) / B for interval length(s) (0.9) :
$Probability
5% 95%
-0.09560675 1.06632725
解釈図
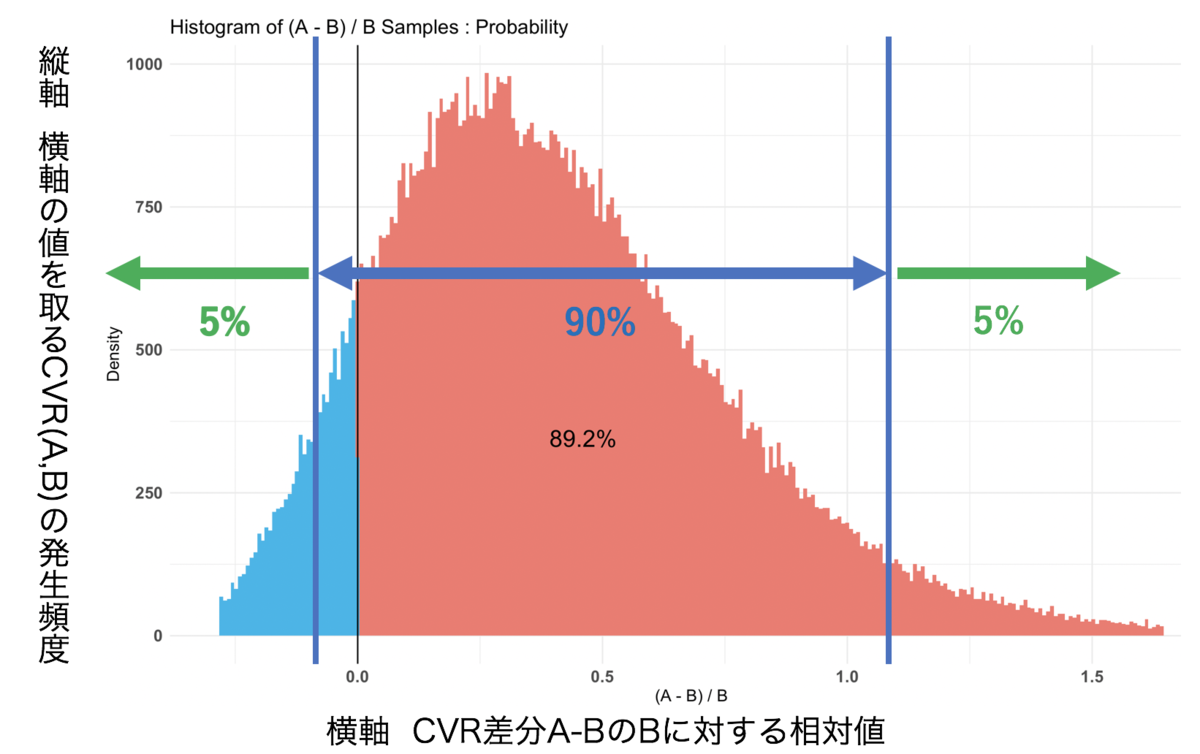
ここの数値では、AページをBページと比較した際に、5%の確率でAページが90.5%以下で悪化させることを示しています。 また、AページをBページと比較した際に、5%の確率でAページが206.6%以上の効果が出ることを示しています。
これらの結果と結果1の数値を考慮すると、AページをBページと比較した際に、Aページの方が89.2%の確率でCVRの効果が期待できると判定することができます。
このように、BayesianABテストの検証では、サンプルサイズが小さい場合でもいい結果が得られる確率と信用区間に対する効果の2つの結果から検証をすることができます。
そのため、サンプルサイズが小さい時の検証には、カイ2乗検定よりもBayesianABテストがむいていると思います。
おわりに
感想
BayesianABテストを調査&実践してみて、大学時代に勉強したことが結構でてきたので、学生時代にちゃんと取り組んでよかったなぁと思いました。いろんな場面で統計学は使えると感じたので、これからも統計については追っていきたいと思います。
次挑戦すること
今回は1つ1つコマンドを入力してBayesianABテストを行っていましたが、次はGASなどを使ってスプレッドシートから自動で検証をしていきたいと考えています。
最後までお読みいただき、ありがとうございました。